Analiza danych a odpowiednia biblioteka w języku Python
Jeżeli kiedykolwiek zdarzyło ci się wykonywać analizę danych, to wiesz, jak ważne jest przedstawienie wyników pracy w sposób szybki i czytelny. Możesz łatwo zobrazować pewne wzorce, anomalie i trendy, które są wynikiem twojej pracy. Jest to szczególnie przydatne w przygotowaniu prezentacji lub raportów biznesowych dla osób nietechnicznych. Wizualizacja wyników pozwala na łatwiejsze przedstawienie obserwacji, a korzystając z narzędzi dostarczonych przez bibliotekę Matplotlib, masz pewność, że cały proces jest wydajny, prosty i elastyczny. Za pomocą kilku linijek kodu otrzymujesz dostęp do podstawowych i zaawansowanych funkcji, które są bezpłatne, bo Matplotlib jest biblioteką open-source.
Szczególnie wydajne jest połączenie możliwości tej biblioteki z innymi bibliotekami naukowymi, takimi jak NumPy, Pandas czy SciPy.
Zakładam, że znasz podstawy języka Python. Jeżeli nie, to nie przejmuj się, ponieważ kod, który tutaj przedstawiam, możesz łatwo zrozumieć i uruchomić po przejściu jednego z kursów programowania w języku Python dostępnych w sieci. Podstawowa składnia wystarczy ci do skorzystania z tego artykułu. Przejdźmy więc do instalacji i konfiguracji środowiska.
Instalacja biblioteki Matplotlib
Na komputerze powinien znajdować się zainstalowany Python w wersji 3.x.
Bibliotekę Matplotlib możesz zainstalować za pomocą menedżera pakietów ‘pip’. Otwórz terminal lub wiersz poleceń (lub PowerShell) dla systemu Windows i wpisz komendę:
pip install matplotlib
Jeżeli korzystasz z Pythona 2.x to skorzystaj z komendy ‘pip2’.
Niektórzy użytkownicy używają narzędzia Anaconda lub Miniconda. W tym przypadku skorzystaj z menadżera pakietów ‘conda’:
conda install matplotlib
W przypadku poprawnego zakończenia procesu instalacji możemy zaimportować bibliotekę do naszego projektu. Zazwyczaj importuje się główny moduł tej biblioteki, czyli ‘pyplot’. Zawiera on niezbędne funkcje do generowania wykresów.
import matplotlib.pyplot as plt
Sama biblioteka korzysta z domyślnych stylów podczas „upiększania” i modyfikacji wykresów. Są to np. modyfikacje kolorystyczne, czcionki, dodawanie dodatkowych informacji, legend itd. Jeżeli chcesz zapoznać się z różnymi stylami, które oferuje Matplotlib, to zajrzyj do dokumentacji lub skorzystaj z komendy ‘print’:
print(plt.style.available)
W celu użycia konkretnego stylu w twoim projekcie skorzystaj z funkcji:
plt.style.use(‘nazwa_stylu’) # np. ‘seaborn’
Konfigurację możesz dostosować według własnych preferencji, modyfikując konkretne wartości parametrów z użyciem funkcji:
plt.rcParams.update({'font.size': 10, 'figure.figsize': (10, 8)})
W tym artykule będę korzystał z domyślnego stylu, ale zachęcam cię do wybrania i dostosowania tego, który najbardziej ci odpowiada. Przejdźmy teraz do podstaw tworzenia wykresów w Matplotlib.
Podstawy tworzenia i omówienie struktury wykresów
Koncepcję i strukturę wykresu w bibliotece Matplotlib najprościej można wyjaśnić za pomocą wykresu liniowego. Wykresy tworzone są na podstawie tzw. Figur ‘figure’. Figura może zostać opisana jako kontener na jedną lub więcej osi ‘axes’. Osiami określamy powierzchnię wykresu, na której rysowane są dane. Jeżeli mowa o wykresie 2D, to zawierał on będzie osie X i Y, a np. wykres 3D X, Y i Z. Do danego wykresu przypisać można również elementy opisujące. Mogą to być etykiety osi, legendy, tytuły i wartości, np. nad słupkami.
W celu utworzenia prostego wykresu liniowego skorzystamy ze wspomnianej wcześniej biblioteki NumPy (odsyłam do mojego poprzedniego artykułu). Stworzymy listę zawierającą wartości liczbowe dla osi X oraz skorzystamy z wartości funkcji sinus dla osi Y.
import numpy as np import matplotlib.pyplot as plt # Przygotowanie danych x = np.linspace(0, 10, 100) y = np.sin(x)
W celu utworzenia wykresu liniowego o krzywej sinusoidalnej użyjemy funkcji ‘plot()’, a następnie wyświetlimy go za pomocą funkcji ‘show()’. Jeżeli uruchomisz poniższy kod, to powinien wyświetlić ci się na ekranie wykres liniowy, który przedstawia funkcję sinus.
plt.plot(x, y) # Rysowanie wykresu liniowego plt.show() # Wyświetlenie wykresu

Jak się pewnie domyślasz, wykres ten nie jest zbyt czytelny, ponieważ poza wartościami same osie nie zostały opisane, wykres nie posiada tytułu, a więc nie jesteśmy w stanie określić, co on tak naprawdę przedstawia. Możemy się domyślać, że chodzi o funkcję sinus, ale lepiej poprawić ten wykres, żeby był bardziej czytelny, szczególnie dla osoby bez znajomości wybranych zagadnień matematycznych. Dodamy zatem tytuł wykresu ‘title()’, etykiety osi ‘xlabel()’, ‘ylabel()’ oraz legendę.
plt.plot(x, y, label='sin(x)') # Dodanie etykiety dla serii danych (do legendy)
plt.xlabel('X') # Etykieta osi X
plt.ylabel('Y') # Etykieta osi Y
plt.title('Wykres funkcji sinus') # Tytuł wykresu
plt.legend() # Dodanie legendy
plt.show() # Wyświetlenie wykresu

Wiesz już, jak stworzyć prosty wykres liniowy, ale co w przypadku gdy istnieje potrzeba prezentacji danych za pomocą innych wykresów? Zajmiemy się nimi w dalszej części, gdzie omówię wybrane ich rodzaje.
Popularne rodzaje wykresów w Matplotlib
Omawiana biblioteka pozwala na dostosowanie naszych wizualizacji do konkretnego przypadku, a przykłady, które podaję, to tylko niektóre z oferowanych możliwości. Jeżeli spędzisz z tą biblioteką więcej czasu, to z pewnością poznasz wiele więcej funkcji i możliwości, a to przełoży się na jeszcze lepsze przedstawianie danych i intuicyjne przekazywanie informacji.
Poza wykresem liniowym popularne są także:
- Wykresy punktowe (Scatter plot) – zbiór punktów, które nie są ze sobą połączone. Używany w wizualizacji korelacji pomiędzy zmiennymi, rozkładu wartości albo określania grup. Przykładem zastosowania może być analiza badania demograficznego pod kątem zależności między wiekiem a zarobkami lub doświadczeniem grupy badanej. Poniżej znajduje się fragment kodu, który pozwala utworzyć wykres punktowy.
import numpy as np
import matplotlib.pyplot as plt
# Przykładowe dane
wiek = np.random.randint(18, 65, 100)
zarobki = np.random.normal(50000, 10000, 100) + (wiek - 18) * 1000
plt.scatter(wiek, zarobki)
plt.xlabel('Wiek')
plt.title('Związek między wiekiem a rocznymi zarobkami')
plt.show()

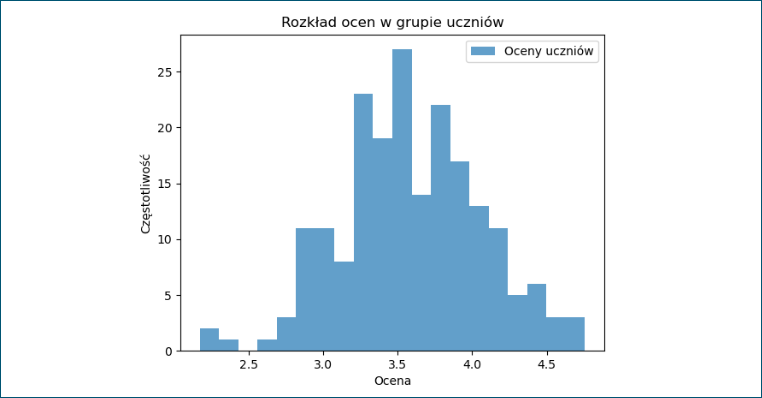
2. Histogram – jest rodzajem wykresu słupkowego, który ilustruje rozkład wartości danych. Wykorzystywany do wizualizacji częstotliwości występowania wartości w wybranym zbiorze danych. Prostym przykładem może być wizualizacja rozkładu ocen w grupie uczniów. Poniżej zamieszczam kod, za pomocą którego wygenerujesz histogram.
oceny = np.random.normal(3.5, 0.5, 200)
plt.hist(oceny, bins=20, alpha=0.7, label='Oceny uczniów')
plt.xlabel('Ocena')
plt.ylabel('Częstotliwość')
plt.title('Rozkład ocen w grupie uczniów')
plt.legend()
plt.show()
3. Wykres słupkowy – jeden z najpopularniejszych wykresów, który przedstawia dane za pomocą poziomych lub pionowych słupków. Zazwyczaj ułatwia porównanie danych, które pogrupowano w konkretne kategorie. Przykładem może być porównanie średnich wyników drużyn w lidze sportowej. Poniżej zamieszczam kod i zrzut ekranu przykładowego wykresu.
plt.bar(druzyny, srednie_wyniki, alpha=0.7)
plt.xlabel('Drużyny')
plt.ylabel('Średni wynik')
plt.title('Porównanie średnich wyników drużyn w lidze sportowej')
plt.show()

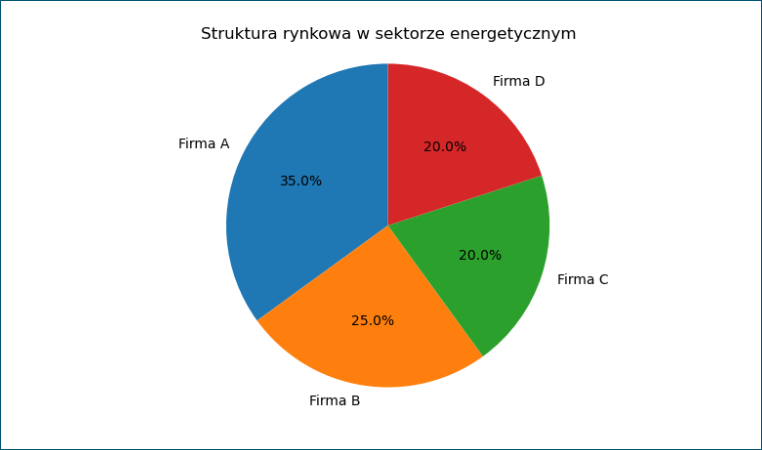
4. Wykres kołowy – dane znajdują się w sektorach w obrębie koła. Doskonale obrazuje proporcje poszczególnych elementów lub grup względem całości. Przykładem może być wykres na podstawie analizy udziału dostawców energii na rynku w Unii Europejskiej. Kod i wykres zostały zamieszczone poniżej.
firmy = ['Firma A', 'Firma B', 'Firma C', 'Firma D']
udzialy_rynku = [35, 25, 20, 20]
plt.pie(udzialy_rynku, labels=firmy, autopct='%.1f%%', startangle=90)
plt.axis('equal')
plt.title('Struktura rynkowa w sektorze energetycznym')
plt.show()
5. Mapa ciepła (heatmap) – nie jest typowym wykresem znanym np. ze szkoły, ponieważ występuje w postaci macierzy, na której kolory odpowiadają wartościom konkretnych komórek. Dobrze obrazuje korelacje i gradienty wartości oraz wykrywa wzorce w przypadku danych dwuwymiarowych. Przykładem użycia może być poziom ekspresji genów w zależności od stworzonych warunków eksperymentalnych.
data = np.random.rand(10, 10)
plt.imshow(data, cmap='hot', interpolation='nearest')
plt.colorbar()
plt.title('Mapa ciepła (heatmap)')
plt.show()
# Mapa ciepła dla ekspresji genów
geny = 50
warunki = 10
ekspresja_genow = np.random.rand(geny, warunki)
plt.imshow(ekspresja_genow, cmap='coolwarm', aspect='auto')
plt.colorbar()
plt.xlabel('Warunki eksperymentalne')
plt.ylabel('Geny')
plt.title('Poziomy ekspresji genów w warunkach eksperymentalnych')
plt.show()

6. Wykres konturowy – używany jest do obrazowania danych trójwymiarowych w postaci linii poziomicy na powierzchni dwuwymiarowej. Wizualizuje wartości, które są równe dla konkretnej funkcji na danej płaszczyźnie. Przykładem może być np. wizualizacja danych pogodowych lub wartości ciśnienia atmosferycznego na mapie meteorologicznej.
x = np.linspace(-10, 40, 100) # długość geograficzna dla Europy (w przybliżeniu)
y = np.linspace(35, 70, 100) # szerokość geograficzna dla Europy (w przybliżeniu)
X, Y = np.meshgrid(x, y)
cisnienie = 1000 + 10 * np.sin(np.sqrt((X - 10)**2 + (Y - 50)**2))
plt.contour(X, Y, cisnienie, levels=20, cmap='coolwarm')
plt.xlabel('Długość geograficzna')
plt.ylabel('Szerokość geograficzna')
plt.title('Ciśnienie atmosferyczne na mapie meteorologicznej')
plt.colorbar(label='hPa')
plt.show()

7. Wykres 3D – powierzchniowy dla funkcji dwóch zmiennych, w tym przypadku funkcji sinusoidalnej na siatce punktów.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Definiowanie danych
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = np.sin(np.sqrt(x**2 + y**2))
# Inicjalizacja wykresu 3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Tworzenie wykresu powierzchniowego
surf = ax.plot_surface(x, y, z, cmap='plasma', edgecolors='k', linewidth=0.5)
# Dodanie paska kolorów
cbar = fig.colorbar(surf, pad=0.15, shrink=0.5, aspect=5)
cbar.ax.yaxis.set_ticks_position('right')
# Etykiety osi
ax.set_xlabel('Oś X', labelpad=10) # labelpad zapobiega nakładaniu się osi
ax.set_ylabel('Oś Y', labelpad=10)
ax.set_zlabel('Oś Z', labelpad=10)
# Tytuł wykresu
ax.set_title('Wykres powierzchniowy')
plt.show()

Pamiętaj, że powyższe kody i wygenerowane wykresy to tylko przykłady i nie muszą odzwierciedlać realnych sytuacji czy danych. Zachęcam cię do sprawdzenia wszystkich rodzajów wykresów, które szczegółowo opisane są w dokumentacji: Plot types — Matplotlib 3.7.1 documentation.
Znasz już podstawowe rodzaje wykresów i wiesz, jak je tworzyć, dlatego w dalszej części tego artykułu na przykładzie wykresu słupkowego pokażę ci, jak możesz dostosować wizualizacje, wykorzystując kilka dodatkowych elementów, jak siatka, linie pomocnicze i wartości nad słupkami, czyli etykiety (labels).
Dostosowanie wykresu
Poniżej znajduje się prosty wykres ukazujący zestawienie dochodu firmy X na przestrzeni ostatnich 7 lat. Kod i wykres zamieszczam poniżej.
import matplotlib.pyplot as plt
# Przykładowe dane
lata = ['2016', '2017', '2018', '2019', '2020', '2021', '2022']
dochody = [32, 45, 58, 64, 49, 59, 72]
plt.bar(lata, dochody, alpha=0.7)
plt.xlabel('Rok budżetowy')
plt.ylabel('Dochód (tys. PLN)')
plt.title('Zestawienie dochodów w tys. PLN na przestrzeni 7 lat')
plt.plot(lata, dochody)
plt.show()
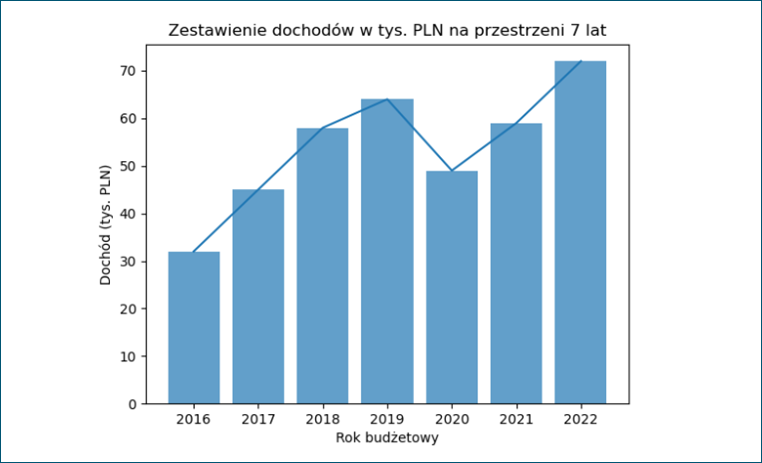
Dodajmy do wykresu kilka dodatkowych elementów, żeby sprawić, by stał się czytelniejszy i odrobinę bardziej atrakcyjny wizualnie.
import numpy as np
import matplotlib.pyplot as plt
# Przykładowe dane
lata = ['2016', '2017', '2018', '2019', '2020', '2021', '2022']
dochody = [32, 45, 58, 64, 49, 59, 72]
x_pos = np.arange(len(lata))
bars = plt.bar(x_pos, dochody, alpha=0.7)
plt.xticks(x_pos, lata)
plt.xlabel('Rok budżetowy')
plt.ylabel('Dochód (tys. PLN)')
plt.title('Zestawienie dochodów w tys. PLN na przestrzeni 7 lat')
plt.plot(lata, dochody,
color='red',
linestyle='--',
linewidth=3,
marker='o',
markersize=10,
label='Linia')
plt.grid(True, linestyle='--', linewidth=0.5, alpha=0.7, color='black')
plt.gca().set_facecolor('whitesmoke')
for bar in bars:
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width() / 2, height + 1, str(height), ha='center', va='bottom')
plt.show()

W powyższym przykładzie na uwagę zasługuje funkcja ‘text()’, która znajduje się w pętli ‘for’. Wspomniana funkcja dodaje wartości nad każdym ze słupków wskazujących na dochód w poszczególnych latach. Jako argumenty przekazujemy położenie na osi X (bar.get_x() + bar.get_width() / 2) oraz położenie na osi Y (height + 1), a także tekst, który ma wyświetlić się nad słupkami (str(height)) i parametry wyrównania tekstu wobec współrzędnych, odpowiednio ‘ha’ – horizontal alignment i ‘va’ – vertical alignment. W celu zapoznania się z innymi metodami i rodzajami nakładania etykiet (wartości) w wykresach słupkowych, ale też innych rodzajach wykresów, odsyłam do dokumentacji Matplotlib: Bar Label Demo — Matplotlib 3.7.1 documentation.
Wykresy wieloosiowe
Czasami zdarzy się, że na jednej figurze (nie mylić z wykresem) chcesz umieścić dwa lub więcej wykresów. Na przykład, tworzysz prezentację na potrzeby szkolenia matematycznego dla licealistów i chcesz przedstawić wykres funkcji sinus i cosinus. W celu dodania kolejnego wykresu do tej samej figury możemy skorzystać z funkcji ‘add_subplot()’ lub funkcji ‘subplots()’. Oczywiście każdy wykres lub oś będzie trzeba skonfigurować osobno, ale jak już wiesz, nie są to skomplikowane operacje. Kod i wykresy na jednej figurze zamieszczam poniżej:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(6, 6))
# Ustawienie odstępu między wykresami
plt.subplots_adjust(hspace=0.5)
ax1.plot(x, y1, color='blue', label='sin(x)')
ax1.set_xlabel('Oś X')
ax1.set_ylabel('sin(x)')
ax1.legend()
ax2.plot(x, y2, color='red', label='cos(x)')
ax2.set_xlabel('Oś X')
ax2.set_ylabel('cos(x)')
ax2.legend()
plt.show()

Pierwszy wykres (na górze) przedstawia funkcję sinusoidalną sin(x), gdzie wartość na osi X jest przedstawiona przez x, a wartość na osi Y przedstawia sin(x). Wykres ma niebieski kolor linii i etykietę ‘sin(x)’.
Drugi wykres (na dole) przedstawia funkcję cosinusoidalną cos(x), gdzie wartość na osi X jest przedstawiona przez x, a wartość na osi Y przedstawia cos(x). Wykres ma czerwony kolor linii i etykietę ‘cos(x)’.
Oba wykresy są umieszczone w jednej kolumnie i dwóch wierszach, ze wspólną osią X, która przedstawia zakres wartości x od 0 do 10. W kolejnym przykładzie pokażę ci nałożenie wykresów na siebie.
Wieloosiowe wykresy mogą być przydatne w różnych zastosowaniach, takich jak:
- Porównywanie różnych wielkości na jednym wykresie.
- Przedstawianie wielkości w różnych jednostkach lub zakresach wartości.
- Prezentowanie danych związanych z czasem, gdzie wartości dla różnych wielkości mają wspólną oś czasu.
Poniżej przedstawiam przykład z nałożonymi krzywymi (sinus i cosinus) na jednym wykresie.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
fig, ax1 = plt.subplots(figsize=(8, 4)) # figsize pozwala na ustalenie rozmiaru figury
# Rysowanie sinusa na pierwszej osi
ax1.plot(x, y1, color='blue', label='sin(x)')
ax1.set_xlabel('Oś X')
ax1.set_ylabel('sin(x)', color='blue')
ax1.tick_params(axis='y', labelcolor='blue')
# Tworzenie drugiej osi dla cosinusa
ax2 = ax1.twinx()
ax2.plot(x, y2, color='red', label='cos(x)')
ax2.set_ylabel('cos(x)', color='red')
ax2.tick_params(axis='y', labelcolor='red')
# Dodawanie legendy
fig.legend(loc='upper right')
plt.grid(True, linestyle='--', linewidth=0.5, alpha=0.7, color='black')
plt.title('Wykres wieloosiowy z sin(x) i cos(x)')
plt.show()

W powyższym przykładzie, ax1 jest osią Y dla sin(x), a ax2 jest osią Y dla cos(x). Używając funkcji twinx(), utworzyliśmy drugą oś Y, która współdzieli wspólną oś X z pierwszą osią Y. Następnie narysowaliśmy funkcje sinusoidalną i cosinusoidalną na odpowiednich osiach, używając różnych kolorów dla linii i etykiet. W ten sposób obie funkcje są przedstawione na jednym wykresie z dwiema osiami Y. Rozmiar figury został zmieniony na 8 cali szerokości i 4 cale wysokości za pomocą parametru ‘figsize’. Zachęcam do eksperymentowania z parametrami w celu uzyskania optymalnych rozwiązań. Ponownie odsyłam do dokumentacji w celu zapoznania się z pełnym zakresem parametrów.
Podsumowanie i cheat sheet
Myślę, że w tym artykule udało mi się pokazać ci podstawy tworzenia wykresów i pracy z biblioteką Matplotlib. Zebrałem też najważniejsze funkcje i fragmenty kodu, które możesz wykorzystać podczas pracy z wizualizacjami, korzystając z Matplotlib.
Importowanie biblioteki:
import matplotlib.pyplot as plt
Tworzenie wykresów:
# Wykres liniowy plt.plot(x, y) # Wykres punktowy (scatter plot) plt.scatter(x, y) # Histogram plt.hist(x, bins) # Wykres słupkowy (bar plot) plt.bar(x, y) # Wykres kołowy (pie chart) plt.pie(values, labels=labels) # Heatmap plt.imshow(matrix, cmap='hot') # Wykres konturowy (contour plot) plt.contour(X, Y, Z)
Wyświetlanie wykresu:
plt.show()
Formatowanie wykresów:
# Tytuł wykresu
plt.title("Tytuł")
# Etykiety osi
plt.xlabel("Oś X")
plt.ylabel("Oś Y")
# Legenda
plt.legend()
# Siatka (grid)
plt.grid()
# Ograniczenie zakresu osi
plt.xlim(min_x, max_x)
plt.ylim(min_y, max_y)
# Skala logarytmiczna
plt.xscale('log')
plt.yscale('log')
Personalizacja wykresów:
# Kolor linii plt.plot(x, y, color='red') # Styl linii (liniowy, przerywany, kropkowany) plt.plot(x, y, linestyle='-') plt.plot(x, y, linestyle='--') plt.plot(x, y, linestyle=':') # Znaczniki punktów plt.plot(x, y, marker='o') plt.plot(x, y, marker='x') plt.plot(x, y, marker='+') # Grubość linii plt.plot(x, y, linewidth=2)
Tworzenie wykresów wieloosiowych:
# Tworzenie wykresów z wieloma osiami Y
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot(x1, y1, 'g-')
ax2.plot(x2, y2, 'b-')
ax1.set_xlabel('Oś X')
ax1.set_ylabel('y1', color='g')
ax2.set_ylabel('y2', color='b')
Zapisywanie wykresu jako obraz:
plt.savefig("nazwa_pliku.png", dpi=300)
Link do dokumentacji Matplotlib:
Matplotlib documentation — Matplotlib 3.7.1 documentation
